电波在传播中,可能受到长期慢衰落和短期快衰落的影响,如图16示。
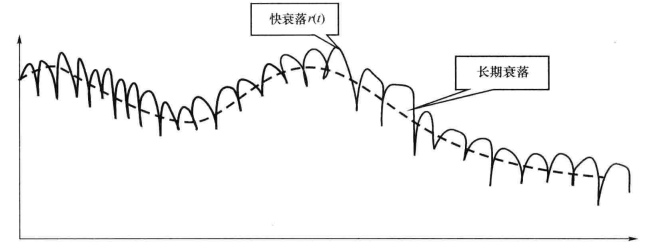
图6 电波传播的长期衰落与短期衰落示意图
(1) 电波传播的长期慢衰落
长期慢衰落是由传播路径上的固定障碍物(如建筑物、山丘、树林等)的阴影引起的,因此也称为阴影衰落或大尺度衰落。阴影引起的信号衰落是缓慢的,且衰落速率与工作频率无关,只与周围地形、地物的分布、高度和物体的移动速度有关。
长期衰落一般表示为电波传播距离的平均损耗(dB)加一个正态对数分量,其表达式为
L=Ld+Xa (10-15)
其中,Ld是距离因素造成的电波损耗;
X。是满足正态分布的随机变量,其均值为0,方差为移动通信环境中竖的典型值为8—10dB。
(2) 电波传播的短期快衰落
由于电波具有反射、折射、绕射的特性,因此接收端接收到的电波信号可能是从发送端发送的电波经过反射、折射、绕射的信号的叠加,即接收信号是发送信号经过多种传播途径的叠加信号。另外反射、折射、绕射物体的位置可能随时间的变化而变化,因此接收信号接收到的多径信号可能在这一时刻与下一时刻不同,在电波频率较高时,微小的距离变化引起多径叠加信号强度的快速变化,即接收端接收到的信号具有快速时变特性,这种特性称为短期快衰落或小尺度衰落。无线通信中的电波传播经常受到这种多径时变的影响。
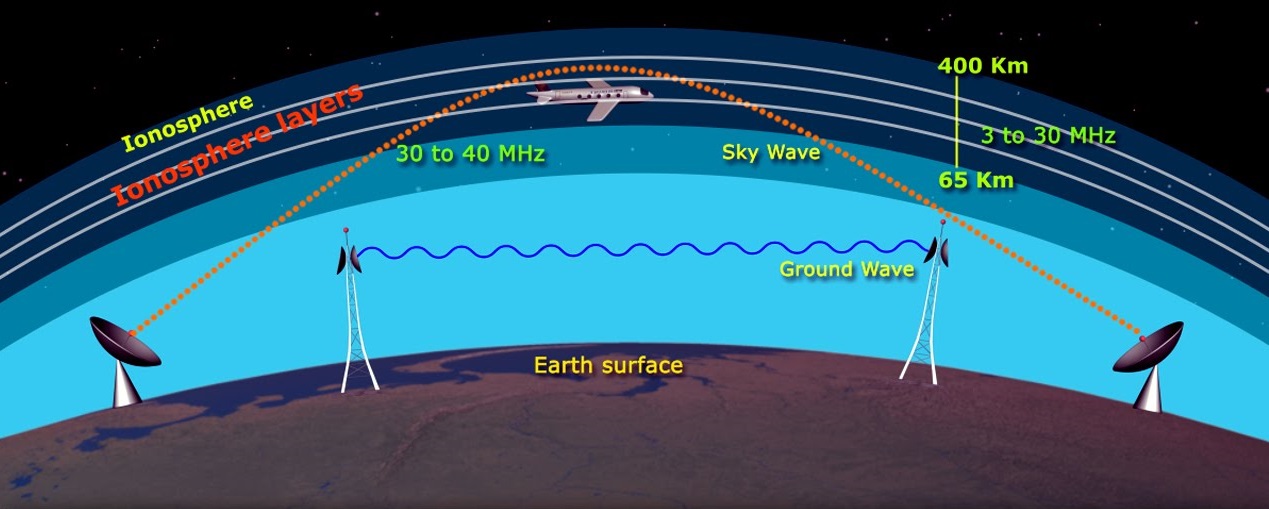

考察信道对发送信号的影响,发送信号一般可以表示成
假设存在多条传播路径,且与每条路径有关的是时变的传播时延和衰减因子,则接收到带通信号为
式(10-17)中,an(t)是第n条传播路径的时变哀减因子;
tn(t)是第n条传播路径的时变传播时延;
st(t)是发送信号的等效低通信号;
可以看出,接收信号的等效低通信号为
而等效低通信道可用如下的时变冲激响应表示
对于某些信道.把接收信号看成由连续多径分量组成的更合适,其等效低通信道为
此时的接收信号为
①信道的时变性
发送信号经过无线信道时,受到时变因素的影响,如式(10-19)中所示,各条传播路径的衰减幅度、传播时延都是随时间变化的,这种变化的因素可能是周围反射物、折射物、绕射物的移动或其他因素引起的。这样,发送信号在前一时刻经受的衰落与下一时刻经受的衰落可能不同,即信道条件随时间变化,造成了时变性。
描述信道的时变快慢经常采用信道的相干时间时或多普勒频移人来描述。当发送信号的码元时间T,与多普勒频移/d的乘积远小于1时,即此时在每个码元时间内,信号的时变因素可以忽略,称此时发送信号经历慢衰落;当发送信号的码元时间T,与多普勒频移入的乘积与1可比时,此时每个码元时间内,信号的时变因素不可以忽略,发送信号经历快衰落。通常,信道的时变性与信号的发送速率相比慢得多,因此实际中相对于一个码元时间内往往可以看成是时不变的。
多普勒频移是根据电波传播的多普勒效应来计算的。多普勒效应是为纪念ChristianDoppler而命名的,他于1842年首先提出了这一理论。他认为声波频率在声源移向观察者时会变高,而在声源远离观察者时会变低。一个常被使用的例子是火车,当火车接近观察者时,其汽鸣声会比平常更刺耳。你可以在火车经过时听出刺耳声的变化。同样的情况还有:警车的警报声和赛车的发动机声。


把声波视为有规律间隔发射的脉冲,可以想象若你每走一步,便发射了一个脉冲,那么在你之前的每一个脉冲都比你站立不动是更接近你自己。而在你后面的声源则比原来不动时远了一步。或者说,在你之前的脉冲频率比平常变高,而在你之后的脉冲频率比平常变低了。
多普勒效应不仅仅适用于声波,它也适用于所有类型的波,包括无线电和光波等。当移动体在X轴上以速度u移动时引起多普勒(Doppler)频率漂移。用一个平面波表示稳定扩散事件,假定x~y平面是平面场,如图10.7所示。
此时,多普勒效应引起的多普勒频移可表示为
式(10-21)中:υ为移动速度;
λ为波长;
a为入射波与移动台移动方向之间的夹角; 为最大多普勒(Doppler)频移。
为最大多普勒(Doppler)频移。
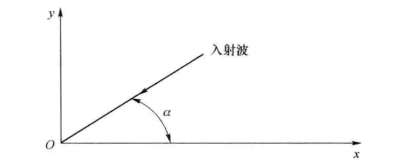
图7 入射波和移动方向
②信道的多径特性
现在来观察一个两径的信道的例子,例如
其傅氏变换为
图8示意了上述两径信道的幅频响应。
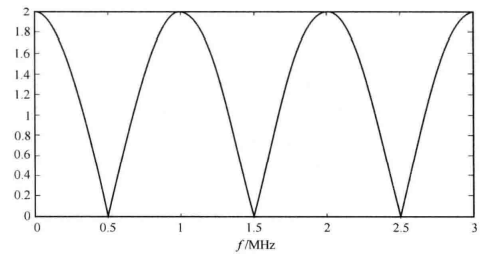
图8 两径信道的幅频响应示意图
从图10.8中可以看到,当发送信号的频带宽度大于0.5MHz时,此时由于信道引起严重的频率选择性衰落,即信号的某些频率分量被严重衰减,某些分量被放大。这种频率选择性衰落对宽带信号传输十分不利,如果没有采用措施进行补偿,则接收到的信号具有严重的失真。
多径引起信道的频率选择性,表征信道的这种特征经常用信道的多径时延扩展r„.这个参数来描述。当发送信号的带宽B与多径时延扩展τm的乘积远小于1时,即Bτ≤1信号的带宽相对于多径的选择性带宽而言很小,通常称此时信号经历平衰落;当发送信号的带宽B与多径时延扩展τm的乘积与1可比时,此时发送信号的带宽与多径的选择性带宽具有可比性,通常称此时信号经历频率选择性衰落。
例如地面微波中继通信信道可以等效成一个两径模型,其中一径是直射路径分量(LOS),另外一径来自周围地形的反射。1979年.Rummler开发出一种基于信道测量的2径模型,该测量是在6GHz频带的典型LOS链路上进行的,测量得到的信道转移函数可以建模为
式(10-22)中:
a为总衰减参数,其分布可用对数正态分布来描述;
β为由多径分量引起的形状参数,其分布具有(I-β)2'3的形式;
f0为衰落最小的频率;
t0为直射路径与反射路径的时延差,其典型值为6.3ns。
对于β>0.5,—201ga的均值为25dB,标准偏差为5dB;对于较小的β值,一20lga的均值为15dB,标准偏差为5dB。
③ 信道衰落的分布
由式(10-19)所示,信道的等效包络基本反映了接收信号的包络,即接收信号的起伏特性。当多径数很大,且每径的衰减和时延是随机时,根据大数定理,信道可以等效成一个复高斯的随机过程,此时由于复高斯的幅度呈瑞利分布(Rayleigh),因此通常称之为瑞利衰落信道;当多径结构中具有明显的直射路径或有明显的强径时,此时信道可以等效成一个正弦波加复高斯的随机过程,此时信道的幅度为莱斯分布,称之为莱斯(Rice)衰落信道;另外一种表征通过多径信道传输的信号的起伏的统计特性的分布是Nakagami分布。
④ 中断率和衰落余量
通信系统的误码率是信噪比的函数,在衰落信道中信噪比是时变的,因此瞬时误码率也是时变的。当信噪比低于某个限值九时,此时的信道将处于不能满足要求的状态,称为“中断中断出现的时间比率叫中断率(OutageRate),或者叫瞬断率。通常的计算方式是
Pt(A)表示事件A发生的概率。假设接收功率为Pmm时恰好Pe=lX10-3,那么中断率就是
P是实际接收电平。由于衰落的原因,P是随机变量。
为了保证中断率低于一定的指标,平时的接收电平应该比最少需要的接收功率留出有些余量。留的余量越多,中断率也就越小。





