天才是百分之一的灵感加上百分之九十九的汗水。
——爱迪生(T.A.Edison)
一、奈奎斯特脉冲整形概念——使信号频谱局限在最小频谱带宽内
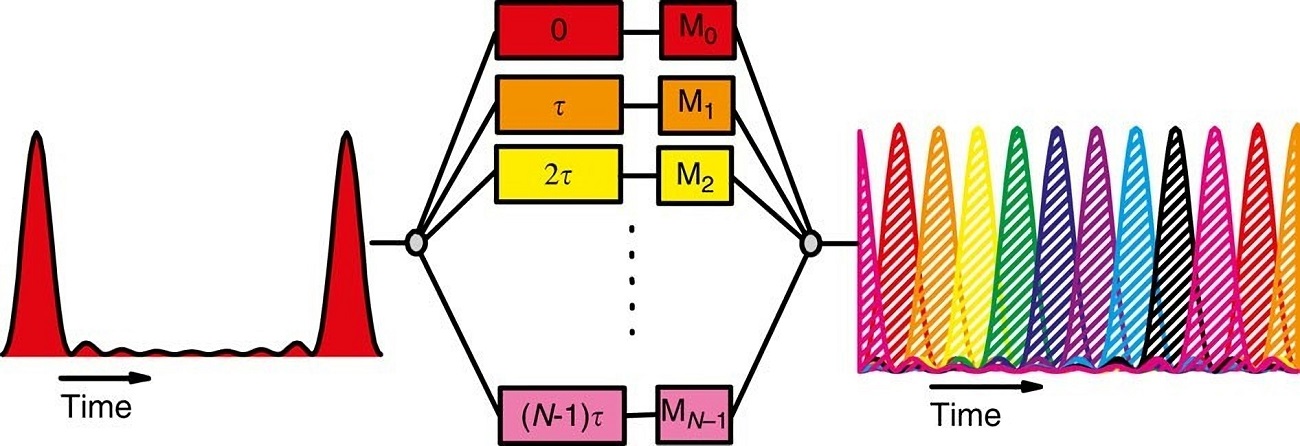
奈奎斯特脉冲整形使信号频谱局限在一个最小可能的频谱带宽内,从而避免信道间的干扰,减少使用专门信号处理技术的需要,允许信道间距接近符号率。它是光纤通信系统提高频谱效率的有效工具,用于构成最密集的WDM系统。
所谓奈奎斯特脉冲整形,就是把时域脉冲形状整形为辛格函数[sinc(x)]形状。辛格函数用sinc(x)=sin(x)/x(x≠0)表示,在数字信号处理器(DSP)和信息论中,通常定义归一化辛格函数为

当x=0时,sinc=1。
在介绍辛格函数频谱特性前,先来回顾一下矩形脉冲的特性。矩形脉冲是最重要和最常用的脉冲信号之一,因为它可以方便地表示二进制数据“1”和“0”。对表示单个矩形脉冲函数进行傅里叶变换,就得到矩形脉冲的频谱为辛格函数形状。图10.5.1a表示矩形脉冲的时域图和对应的频域图,由图可见,脉冲宽度T与频谱图中的第1个零点位置1/T是反比关系。
利用傅里叶变换的对称定理,很容易得知,具有sin(x)/x形状的辛格脉冲信号的频谱为矩形频谱,如图10.5.1b所示。
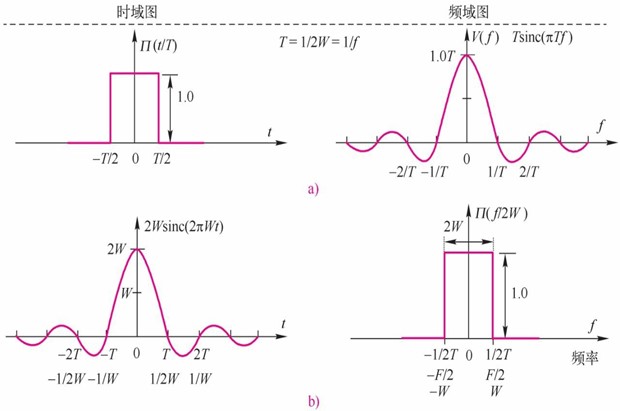
图10.5.1矩形脉冲和辛格脉冲及其频谱(傅里叶变换对应的时域和频域信号)
a)矩形脉冲(不整形)b)辛格脉冲(整形后的奈奎斯特脉冲)
由此可见,在时域,奈奎斯特脉冲形状是辛格函数形状;在频域,它是方波形状。
二、 奈奎斯特发送机/接收机及其系统
奈奎斯特发送机和接收机与传统的不同,它不仅要对数据包络编码到光载波fv上,而且要对脉冲形状编码。因此,需要对发送机输出脉冲整形。
在光脉冲整形和复用发送机中,首先,用I/Q调制器把电信号编码到光载波上,然后,对光信号进行脉冲整形,形成发送机信号脉冲响应函数hs(t)脉冲,进一步波长复用,产生Tbit/s超级信道信号。当然,也可以在电域进行奈奎斯特整形。
图10.5.2表示一个在实验室使用的奈奎斯特光发送机,该实验使用FPGA构成64抽头系数的有限冲激响应(FIR)滤波器,对输入的伪随机码在电域实时进行奈奎斯特脉冲整形,经数模转换(DAC)平滑后,对MZ调制器进行I/Q调制,发送机输出信号的时域图/频域图几乎为辛格状/方形脉冲。接收端为相干接收机,以80GSa/s取样,同时处理两个偏振输入信号,进行模数转换(ADC)、载波相位恢复和时钟估算恢复、增益均衡、色散补偿和BER测量。
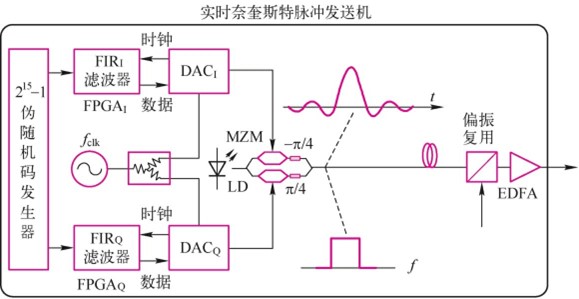
图10.5.2 奈奎斯特脉冲整形传输实验系统光发送机构成图
奈奎斯特脉冲整形允许有效地进行波长复用,无须保护间隔,在这方面类似于正交频分复用,即方形的时域脉冲和辛格状的频域脉冲,如图10.5.1所示。