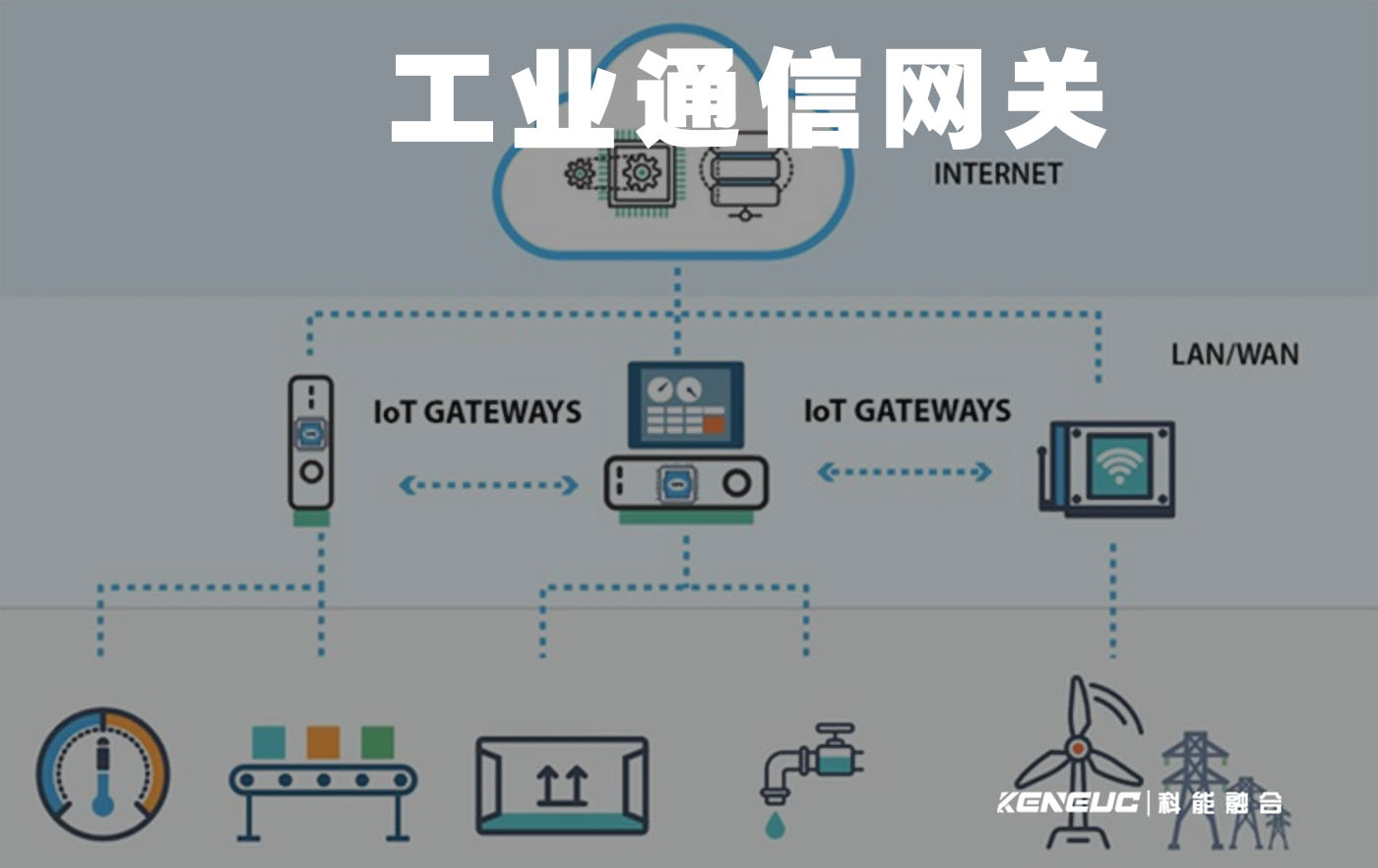
工业通信网关是实现工业物联网互联互通的关键设备。随着工业物联网的快速发展,越来越多的设备和系统需要进行互联互通,而工业通信网关正是实现这一目标的关键组件。本文将介绍工业通信网关的定义、功能、应用场景以及类型。
一、工业通信网关的定义
工业通信网关是一种连接不同通信协议和网络的设备,用于实现工业物联网中各种设备和系统之间的互联互通。它可以将不同协议的数据进行转换和传输,使得不同设备之间可以无缝通信。
二、工业通信网关的功能
网关可以包含协议转换器、阻抗匹配器件、速率转换器、故障隔离器或信号转换器等功能,以提供系统互操作性。本报告中涵盖的工业网关用于将联网设备(无论是否基于IP)引入基于IP的网络,并可能进入工业互联网。
随着工业互联网的出现,工业网关的功能范围正在扩大。过去主要归结为简单的协议转换,但基于远程可编程微处理器的网关平台的出现,具有标准操作系统,能够托管IIoT平台代理和常驻应用程序,极大地扩展了网关的功能。
由于重点关注作为工业互联网边缘基础设施设备的潜在用途,该报告特别关注支持基于IP的网络的网关。这不包括在从站和主站级别仅支持非基于IP的网络的网关,包括许多将非基于IP的(通常是串行自动化网络)相互连接的网关。工业网络网关
ARC进一步排除了连接到基于基于以太网的网络协议的PLC背板的网络接口卡。例如,设计用于基于EtherNet/IP的PLC背板的网络接口卡被排除在外。
网络路由器和交换机通常包含在网关频谱的一部分中,但此类产品被明确排除在本报告中,并包含在单独的ARC网络基础设施可交付成果中。媒体转换器、设备服务器和专用协议转换器同样被排除在外。
工业通信网关具有以下主要功能:
- 协议转换:工业通信网关可以将不同通信协议的数据进行转换,实现不同设备之间的互联互通。例如,将Modbus协议的数据转换为OPCUA协议的数据,使得不同设备可以使用统一的协议进行通信。
- 数据采集:工业通信网关可以连接各种传感器和设备,实时采集数据并进行处理。它可以将采集到的数据发送给上层系统进行分析和监控。
- 安全保护:工业通信网关可以对数据进行加密和认证,确保数据传输的安全性。它可以防止未经授权的访问和数据泄漏,保护工业物联网系统的安全。
- 远程管理:工业通信网关可以通过远程管理平台对设备进行监控和管理。管理员可以通过远程管理平台对设备进行配置和维护,提高系统的可靠性和可管理性。
三、工业通信网关的应用场景
工业通信网关广泛应用于各个工业领域,包括制造业、能源、交通等。以下是几个常见的应用场景:
- 智能制造:工业通信网关可以连接生产设备和管理系统,实现生产数据的采集和监控。通过工业通信网关,生产线上的各个设备可以实现互联互通,提高生产效率和质量。
- 智能能源:工业通信网关可以连接能源监测设备和能源管理系统,实现能源数据的采集和分析。通过工业通信网关,能源管理人员可以实时监控能源消耗情况,优化能源利用效率。
- 智慧交通:工业通信网关可以连接交通设备和交通管理系统,实现交通数据的采集和处理。通过工业通信网关,交通管理人员可以实时监控交通流量和路况,调整交通信号,提高交通运输效率。
四、工业通信网关类型
本报告从所服务的从站和主站网络的角度介绍了网关市场。由于强调工业互联网应用,所有主站网络都必须基于IP,不包括串行和其他非IP主站。按网络类型划分的类别包括:- 以太网主站的无线从站(任何类型的无线网络,包括Wi-Fi、WirelessHART或蓝牙等个人局域网)
- 其他从站到以太网主站(通常为串行自动化网络)
- 无线从站到无线主站(同样可以是任何类型的无线,但通常是蓝牙或等同于Wi-Fi)
- 蜂窝网络(蜂窝网络的任何类型的从站)
结论
工业通信网关是实现工业物联网互联互通的关键设备。它具有协议转换、数据采集、安全保护和远程管理等功能,广泛应用于智能制造、智能能源和智慧交通等领域。通过合理选择和配置工业通信网关设备,可以实现设备和系统之间的无缝通信,提高工业物联网系统的可靠性和可管理性。