1.马赫-曾德尔(M-Z)干涉仪
马赫-曾德尔(M-Z)干涉仪(Mach-Zehnder Interferometer)如图4.1.3 所示,一束相干光在O点被分光器分成两束光,一束光被M1反射镜反射,经过折射率为n、长度为d的试样传输后,进入合光器;而另一束光被M2反射镜反射,也进入合光器,在C点合光后的两束光进行干涉,然后干涉光进入探测器。根据式(2.2.3),在C点的光场强度取决于OAC和OBC之间的光程差
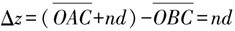
由光程差决定的相位差为

式中,k是光在试样中的传输常数或波数,n是试样材料的折射率,d是试样的长度。当两臂间的相位差Δφ等于π时,两束光在C点出现了相消干涉,探测器输入光为零;当两臂的光程差为0或2π的倍数时,两束光在C点相长干涉,探测器输入光为最大。电光效应晶体试样的折射率n可以通过施加在晶体上的电压来改变,热光效应晶体试样的长度d可以通过加热试样来改变。
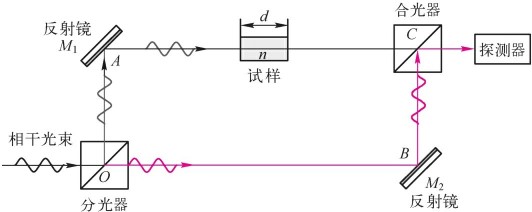
图4.1.3马赫-曾德尔(M-Z)干涉仪
该干涉仪由德国物理学家路德维希·曾德尔(LudwigZehnder)首先于1891年提出构想,次年路德维希·马赫(Ludwig Mach)发表论文对这一构想加以改进,所以该仪器就以马赫和曾德尔的名字命名为马赫-增德尔(M-Z)干涉仪。马赫-曾德尔干涉仪已被广泛应用于光通信中的光调制器中,也广泛应用在量子通信中。
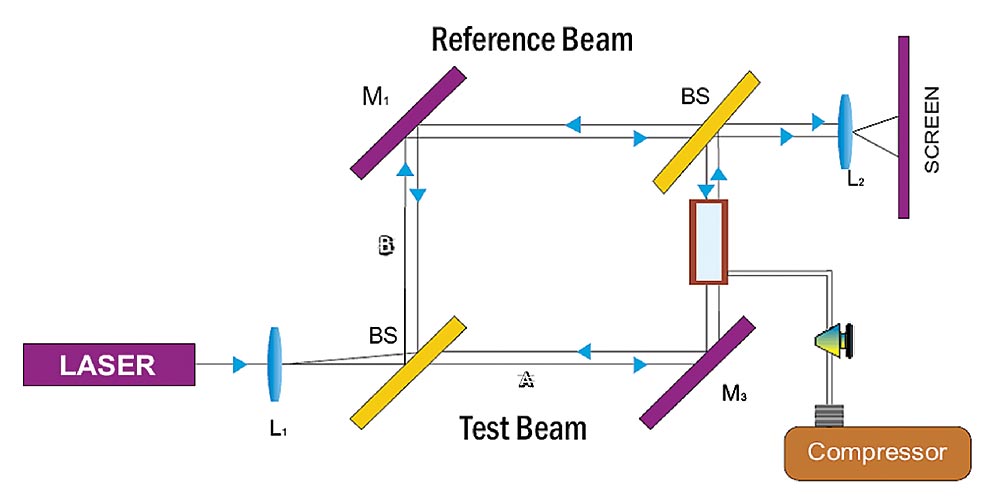
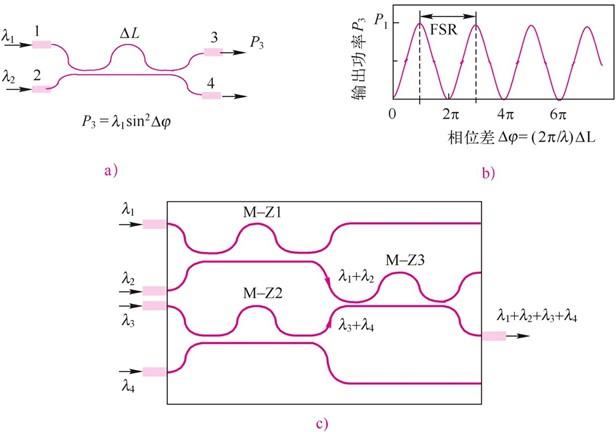
最常用的幅度调制器是在LiNbO3晶体表面用钛扩散波导构成的马赫-曾德尔(M-Z)干涉型调制器,如图4.1.4所示。
马赫-曾德尔干涉仪可以用来观测从同一光源发射的光束分裂成两道准直光束后,经不同路径与介质传输后,产生的相对相移变化使这两束光发生相长干涉或相消干涉现象。
马赫-曾德尔(M-Z)干涉型调制器使用两个频率相同但相位不同的偏振光波进行干涉,外加电压引入相位的变化可以转换为幅度的变化。在图4.1.4a表示的由两个Y形波导构成的结构中,在理想的情况下,输入光功率在C点平均分配到两个分支传输,在输出端D干涉,所以该结构扮演着一个干涉仪的作用,其输出幅度与两个分支光通道的相位差有 关。两个理想的背对背相位调制器,在外电场的作用下,能够改变两个分支中待调制传输光的相位。由于加在两个分支中的电场方向相反,如图4.1.4a的右上方的截面图所示,所以在两个分支中的折射率和相位变化也相反,例如若在A分支中引入π/2的相位变化,那么在B分支则引入-π/2相位的变化,因此A、B分支将引入相位π的变化。
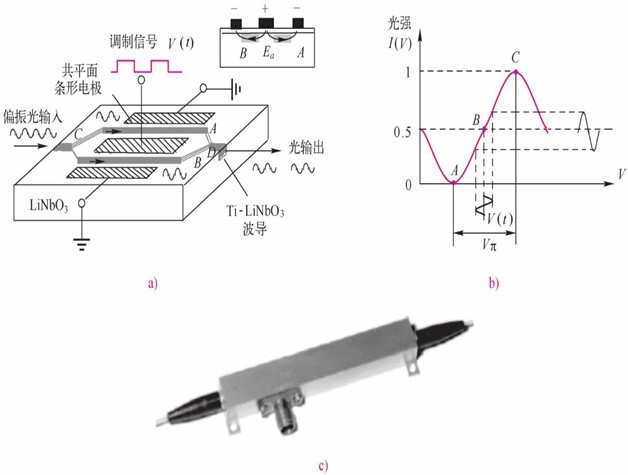
图4.1.4 马赫-曾德尔幅度调制器
a)调制电压施加在两臂上 b)马赫-曾德尔调制器电光响应 c)商用马赫-曾德尔调制器
假如输入光功率在C点平均分配到两个分支传输,其幅度为A,在输出端D的光场为
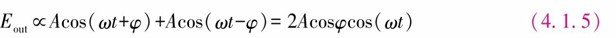
输出功率与 成正比,所以由式(4.1.5)可知,当φ=0时输出功率最大,当φ=π/2时,两个分支中的光场相互抵消干涉,使输出功率最小, 在理想的情况下为零。于是

由于外加电场控制着两个分支中干涉波的相位差,所以外加电场也控制着输出光的强度,虽然它们并不成线性关系。
在图4.1.4a表示的强度调制器中,在外调制电压为零时,马赫-曾德尔干涉仪A、B两臂的电场表现出完全相同的相位变化;当加上外电压后,电压引起A、B波导折射率变化,从而破坏了该干涉仪的相长特性,因此在A、B臂上引起了附加相移,结果使输出光的强度减小。作为一个特例,当两臂间的相位差等于π时,在D点出现了相消干涉,输入光强为零;当两臂的光程差为0或2π的倍数时,干涉仪相长干涉,输出光强最大。当调制电压引起A、B两臂的相位差在0~π时,输出光强将随调制电压而变化,如图4.1.4b所示。由此可见,加到调制器上的电比特流在调制器的输出端产生了波形相同的光比特流复制。图4.1.4c为商用马赫-曾德尔调制器。