根据纤芯直径2a和光波波长λ比值的大小，光纤的传输原理可用光在波导中的光线理论或导波理论进行分析。对于多模光纤，2a/λ远远大于光波波长λ，可用几何光学的光线理论近似分析光纤的传光原理和特性；对于单模光纤，2a可与λ比拟，就必须用麦克斯韦导波理论来进行分析。
全反射和相干——光纤传输条件
由2.3.1节可知，光波从折射率较大的介质入射到折射率较小的介质时，在边界将发生反射和折射，当入射角θi超过临界角θc时，将发生全反射，如图2.3.4c所示。光纤传输电磁波的条件除满足光线在纤芯和包层界面上的全反射条件外，还需满足传输过程中的相干加强条件。因此，对于特定的光纤结构，只有满足一定条件的电磁波可以在光纤中进行有效的传输，这些特定的电磁波称为光纤模式。光纤中可传导的模式数量取决于光纤的具体结构和折射率的径向分布。如果光纤中只支持一个传导模式，则称该光纤为单模光纤。相反，支持多个传导模式的光纤称为多模光纤。
为简单和直观起见，以阶跃型光纤为例，进一步用几何光学方法分析多模光纤的传输原理和导光条件。如图3.2.1所示，光线在光纤端面以不同角度α从空气入射到纤芯（n0<n1），不是所有的光线都能够在光纤内传输，只有一定角度范围内的光线在射入光纤时产生的折射光线才能在光纤中传输。假如在光纤端面的入射角是α，在波导内光线与正交于光纤轴线的夹角是θ。此时，θ>θc（临界角）的光线将发生全反射，而θ<θc的光线将进入包层泄漏出去。于是，为了光能够在光纤中传输，入射角α必须要能够使进入光纤的光线在光纤内发生全反射而返回纤芯，并以曲折形状向前传播。由图3.2.1可知，最大的α角应该是使θ=θc。
在n0/n1界面，根据斯奈尔定律（见2.3.1节）可得
全反射时，由式（2.3.2）可知，sinθc=n2/n1，将此式代入式（3.2.1），可得
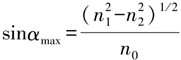
当光从空气进入光纤时，n0=1，所以
定义数值孔径（NA）为
式中，Δ=（n1-n2）/n1为纤芯与包层相对折射率差。设Δ=1%，n1=1.5，得到NA=0.21或θc=12.1°。因此用数值孔径表示的光线最大入射角αmax是
角度2αmax称为入射光线的总接收角，它与光纤的数值孔径和光发射介质的折射率n0有关。式（3.2.4）只应用于子午光线入射，对于斜射入射光线，具有较宽的可接收入射角。多模光纤的大多数入射光线是斜射光线，所以它对入射光线所允许的最大可接收角要比子午光线入射的大。
当θ=θc时，光线在波导内以θc入射到纤芯与包层交界面，折射光线沿交界面向前传播（折射角为90°），如图3.2.1b所示。当θ<θc时，光线将折射进入包层并逐渐消失。因此，只有与此相对应的在半锥角为2αmax的圆锥内入射的光线才能在光纤内传播，所以光纤的受光范围是2αmax。
NA表示光纤接收和传输光的能力，NA（或αmax）越大，光纤接收光的能力越强，从光源到光纤的耦合效率越高。对无损耗光纤，在αmax内的入射光都能在光纤中传输。NA越大，纤芯对光能量的束缚能力越强，光纤抗弯曲性能越好。但NA越大，经光纤传输后产生的输出信号展宽越大，因而限制了信息传输容量，所以要根据使用场合选择适当的NA。
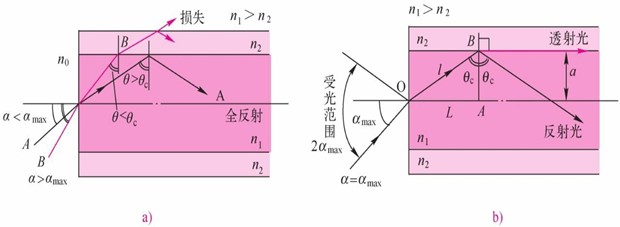
图3.2.1光纤传输条件
a）不同入射角θ的光纤b）θ=θc的光线
一维光纤波导——直线光线
1.光波在波导中传输的条件——全反射和相长干涉
光纤波导横截面是二维（r和φ）尺寸，如图3.2.6所示，反射从所有表面，即从与y轴成 φ角的任意半径方向所碰到的界面发生反射。为了理解光纤的传输理论，先来分析光线在一维（φ=0）光纤波导中的传播，如图3.2.2所示。
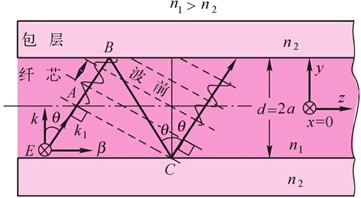
图3.2.2光纤波导中传输的光波必须与它自己相长干涉，否则相消干涉就不会建立起传输光场
由于波导芯的折射率n1大于包层的折射率n2，所以光在光纤波导界面处发生全反射。取电场E方向为沿x方向、平行于界面并正交于z方向。光线以z字形沿z方向向前传播，并在纤芯和包层界面处（如B和C点）全反射，图中用细实线表示出光线恒定的相位波前，它正交于传输方向。光线在C点反射后，反射光线波前正好与在A点的起始光线波前重叠，如果它们不同相，这两束光线将相消干涉，相互抵消。因此只有特定的反射角θ能够发生相长干涉，由此可见，只有特定的波才能在波导中存在。
A和C两点的相位差对应光路径长度AB+BC，而且在A和B点的每次全反射都会产生一个相位差ϕ。假如k1 是光波在n1 介质中的传播常数，k1=kn1=2πn1/λ，式中k和λ分别是自由空间传播常数和波长。为了实现相长干涉，A、C两点间的相位差必须是2π的整数倍，即
Δϕ（AC）=k1（AB+BC）-2ϕ=m（2π），m=0，1，2，…
由图3.2.2可知，BC=d/cosθ，AB=BCcos（2θ），于是
AB+BC=BCcos(2θ)+BC=BC［(2cos2θ-1)+1］=2dcosθ
所以光波在波导中传输的条件是
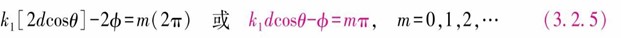
显然，对于给定的m，只有一定的θ和ϕ值才能满足式（3.2.5），ϕ与θ有关，也与光波的偏振态有关。因此对于每个m值，将允许有一个θm和一个相对应的ϕm。因k1=2πn1/λ，d=2a，所以满足波导相长干涉的波导条件式（3.2.5）变成
式中，ϕm表示ϕ是入射角θm的函数。
波矢量k 1可以分解成两个沿波导（z轴）的传播常数β和k，如图3.2.2 所示。设θm满足波导条件，则
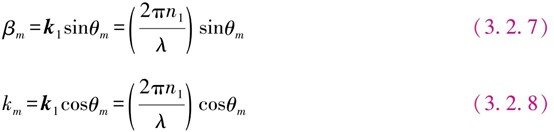
由式（3.2.6）显然可见，只有一定入射角的光线才能在波导内传输，并与m=0,1,2,…对应，而且大的m值产生小的θm角。每个不同的m值将产生不同的由式（3.2.7）决定的传播常数β，m值称为模数。
与式（2.2.1）类似，沿波导传输的光波可用式（3.2.9）来描述
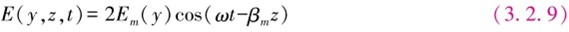
式中，Em（y）表示对于给定的m，电场在z方向传输过程中沿y方向的分布，如图3.2.3所示。图3.2.4表示m=0，1，2三种模式的波沿波导y方向的电场分布，m越大，光场进入包层越深，在包层靠近界面的消逝波以指数形式沿y方向衰减。整个电场沿z方向以各自的传播常数βm传输，从3.1.4节可知它是群速度。图3.2.5表示光脉冲进入波导后分裂成各种模式的波，以不同的群速度向前传输，高阶模传输最慢，低阶模最快，在波导输出端重新复合构成展宽的输出光脉冲。
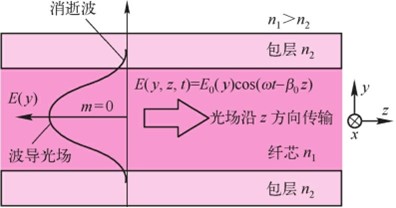
图3.2.3m=0基模光波沿波导y方向的电场分布，通常入射角θ=90°，沿z方向的相速度最大
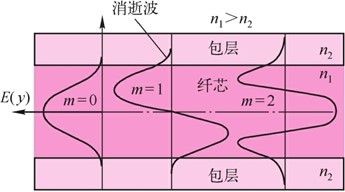
图3.2.4m=0,1,2三种模式的波沿光纤波导y方向的电场分布
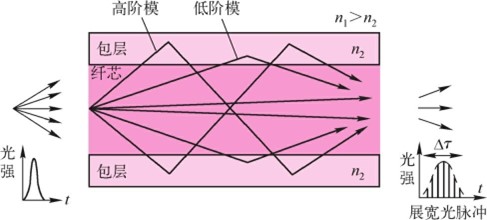
图3.2.5光脉冲进入光纤波导后分裂成各种模式的波
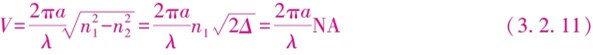
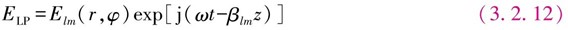
虽然式（3.2.6）规定了光波在波导中传输所允许的入射角，但它还必须同时满足全反射条件sinθm>sinθc，因此在波导中有一个允许在其中传输的最大模数。从式（3.2.6）可以获得sinθm的表达式，并应sinθm>sinθc，得到最大模数m必须满足
式中
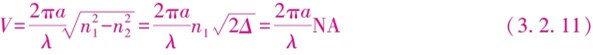
V数也叫作V参数，因为频率与波长成反比，所以叫归一化频率；在光纤波导中，因为d=2a，所以V参数也叫归一化芯径。对于给定的自由空间波长λ，V数取决于波导几何尺寸（d=2a）和波导特性（n1和n2）。从式（3.2.10）和式（3.2.11）可知，要想使模式数量减少，可以减少2a/λ值，或者使n1和n2值更接近些。
二维光纤波导——螺旋光线
光纤波导横截面是二维（r和φ）尺寸，如图3.2.6所示。因为任意方向的半径r均可以用x和y来表示，所以波的相长干涉包括x方向和y方向的反射，因此用两个整数l和m来标记所有可能在波导中存在的行波或导模。
在阶跃折射率光纤中，沿光纤曲折传输的光线，除通过轴线入射的子午光线外（每个反射光线也通过光纤轴线），如图3.2.6a所示，还有非轴线入射的斜射光线，此时反射光线没有通过轴线，而是围绕轴线螺旋式前进，如图3.2.6b所示。
在阶跃多模光纤中，入射的法线光线和斜射光线都产生沿光纤传输的导模，每一个都具有一个沿z方向的传播常数（群速度）β，如图3.2.2所示。法线光线在光纤内产生TE波和TM波，然而斜射光线产生的导模既有横电场Ez分量，又有横磁场Bz分量，因此既不是TE波，也不是TM波，而是HE波或EH波，这两种模的电场和磁场都具有沿z方向的分量，所以称为混合模，如图3.2.6b所示。HE模的磁场分量比电场分量强，而EH模却相反。
图3.2.6光线以法线和斜射入射时在纤芯内以不同的路径传输
a）子午光线总与光纤轴相交b）斜线光线不与轴相交，而是围绕轴曲折前进（螺旋光线），数字表示光线反射的次数
当光纤的折射率差Δ<<1时，称这种光纤为弱导光纤。通常阶跃型光纤Δ≈0.01，所以它是弱导光纤。这种光纤的导模几乎是平面偏振行波，它们具有横电场和横磁场，即E和B互相正交，且垂直于z轴，类似于平面波的场方向，但是场强在平面内不是常数，称这些波为线性偏振
（LP）波，即具有横电场和横磁场的特性。这种沿光纤传输的LP导模可用沿z方向的电场分布E（r,φ）表示，这种场分布或者场斑是在垂直于光纤轴（z方向）的平面内，因此与r和φ有关，而与z方向无关。因此用对应于r和φ两种边界的两个整数l和m来描述其特性。这样在一个LP模中的传输场分布可用Elm（r,φ）表示，称这种模为LPlm模。于是LPlm模就可用沿z方向的行波表示
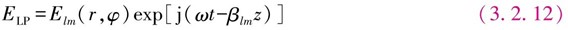
式中，ELP表示LP模的电场，βlm是它沿z方向的传播常数。显然，对于给定的l和m，Elm（r，φ）表示在z轴某个位置上特定的场分布，该场以βlm（群速度）沿光纤传播。
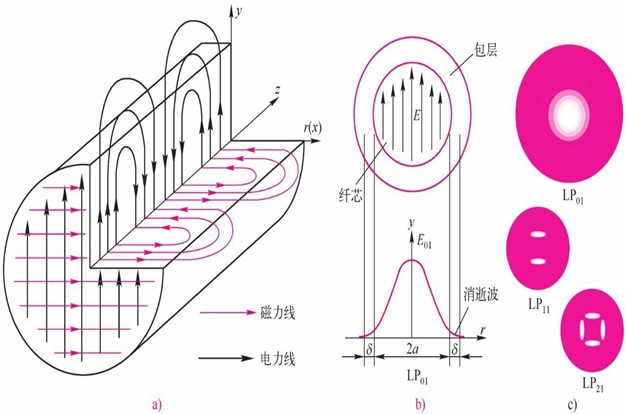
图3.2.7a表示阶跃光纤的基模（E01）电场分布，它对应l=0和m=1的LP01模（即零次模，N=0）。该场在纤芯的中心（光纤轴）最大，由于折射波（含消逝波）的存在，有部分场进入包层，其大小与V参数有关，由式（3.2.11）可知，即与波长有关。各模的光强与E2成正比，这意味着，在LP01模内的光强分布具有沿光纤轴线的最大值，如图3.2.7b所示，在中心最大，向外逐渐减弱，接近包层最小。图3.2.7c也表示出LP11模（即1次模，N=1）和LP21模（即2次模，N=2）的强度分布。l和m对应LPlm模的光强分布图案（场斑），l表示循环一周（φ=360°）最大光强的对数，m表示从纤芯开始沿r方向到包层具有场斑的个数。例如，LP21模表示循环一周有两对场斑，从纤芯到包层有一个场斑。由此可见，l表示螺旋传输的程度，或者说斜射光线对该模贡献的大小，对于LP01（基模）l为零，说明没有斜射光线，对于LP11模，循环一周有一对场斑；m与光线的反射角有关。
图3.2.7阶跃光纤线性偏振（LPlm）各模的电场分布
a）LP01（HE11）模电力线和磁力线在光纤波导中的分布b）LP01模与光纤轴垂直的横截面的电场分布
c）LPlm模与光纤轴垂直的横截面的强度分布
从上面的讨论可知，光以各种传导模沿光纤传输，每种模具有自己的传播常数βlm（即与波长有关的群速度Vg（l,m））、电场分布Elm（r,φ）。当脉冲光射入光纤后，它通过各种导模沿光纤传输，然而每种模式的光以不同的群速度传输，低次模传输快，高次模传输慢，所以到达光纤末端的时间也各不相同，经光探测器转变成光生电流后，各模式混合使输出脉冲相对于输入脉冲展宽，这种色散称为模间色散。色散与光纤波导的结构参数和尺寸（a和Δ）有关，这一点将在3.3.2节进一步讨论，因此可以设计一种只能传输基模的波导，从而也就没有模间色散。
光纤波导是导电率为零的一种圆柱形波导，用3个变量即光纤半径尺寸r、光纤轴方向z和r与y轴的夹角φ表示，如图3.2.6所示，在光纤中传输的光波是电磁波，其运动规律仍遵守麦克斯韦波动方程，它是一种偏微分方程。在柱坐标系中，用拉普拉斯方程表示的光纤波导内的电场为
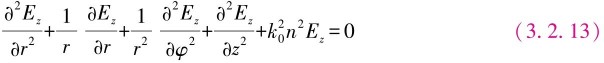
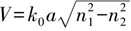
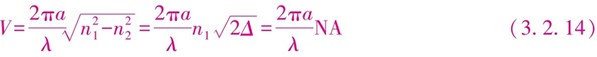
光纤模式——麦克斯韦波动方程求解结果
光纤波导是导电率为零的一种圆柱形波导，用3个变量即光纤半径尺寸r、光纤轴方向z和r与y轴的夹角φ表示，如图3.2.6所示，在光纤中传输的光波是电磁波，其运动规律仍遵守麦克斯韦波动方程，它是一种偏微分方程。在柱坐标系中，用拉普拉斯方程表示的光纤波导内的电场为
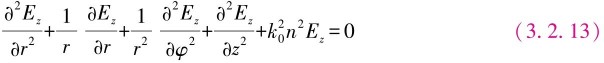
式中，k0为传播常数，n为阶跃光纤折射率，当r≤纤芯半径a时，n=n1；当r＞a时，n=n2。
由光纤波导结构决定的边界条件，用分离变量法将波动方程式（3.2.13）化解为系数为自变量函数的贝塞尔线性方程，然后通过适当的换元法将变系数方程化为常系数方程，便可把光的传播用电磁波表示。
只有满足边界条件所决定的某一相位匹配条件之电磁波，才能被封闭在纤芯内传输，这就是传输模。解波动方程可以得到光纤模式特性、场结构、传播常数和截止条件等。用波动光学分析光波在光纤中的传输结果是，第一类l阶贝塞尔函数Jl(x)可以描述光波在纤芯内的光场分布，它有点像衰减的正弦函数；第一类l阶修正的贝塞尔函数Kl(x)可以描述光波在包层内的光场分布，它有点像衰减的指数函数。对于阶跃折射率光纤，反映其特性的V参数为
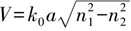
因传播常数k0=2π/λ（见2.2.2节），所以
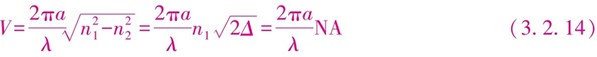
式中，λ是自由空间工作波长，a是纤芯半径，n1和n2分别是纤芯和包层的折射率，NA是光纤的数值孔径，Δ是纤芯和包层的折射率差
由式（3.2.14）可知，V参数与光纤的几何尺寸（芯径）2a有关，所以称为归一化纤芯直径，或简称为归一化芯径；另一方面，V参数又与波长成反比，具有频率的量纲，所以又称为归一化频率，同时又与光纤波导折射率n1和n2有关，因此它是描述光纤特性的重要参数。
引入归一化传播常数b，它与传播常数（群速度）β（β=βlm）的关系是
式中，传播常数（相速度）k=2π/λ，n1和n2分别是纤芯和包层的折射率。
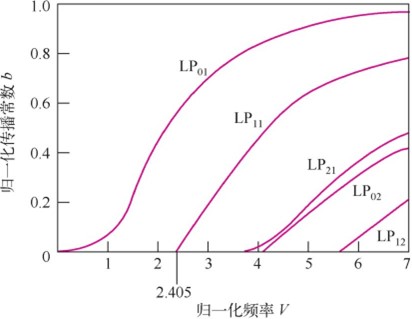
因为LP模的传播常数βlm取决于波导特性和光源波长，因此仅用与V参数有关的归一化传播常数b，描述光在波导中的传输特性是非常方便的。图3.2.8表示几种低阶线性偏振模（LP）的b与V的关系。
图3.2.8几种LP模的归一化传播常数b与归一化频率V的关系
注：LP01为零次模，N=0；LP11为1次模，N=1；LP21为2次模，N=2
由图3.2.8可见，基模LP01对所有的V数都存在，所以LP01在任何光纤中都能存在，是永不截止的模式，称为基模或主模。而LP11在V=2.405截止，对于每个比基模高的特定的LP模，总有一个对应于截止波长的截止V数。给出光纤的V参数，从图3.2.8很容易找到对于允许在波导中存在的LP模所对应的b，接着按式（3.2.16）就可以求得β。
当V<2.405时，只有一种模式即基模LP01通过光纤芯传输，当减小芯径使V数进一步减小时，光纤仍然支持LP01模，但该模进入包层的场强增加了，因此该模的一些光功率被损失掉。这种只允许基模LP01在要求的波长下传输的光纤称为单模光纤。通常单模光纤比多模光纤具有更小的纤芯半径a和较小的折射率差Δ。
当V>2.405时，假如光源波长λ减小得足够小，单模光纤将变成多模光纤，高阶模也将在光纤中传输。因此光纤变成单模的截止波长λc
由
得出
得出
改变阶跃折射率光纤的各种物理参数可能对传输模数量的影响可从式（3.2.10）和式（3.2.14）推断出来，例如，增加芯径（a）或者折射率（n1）可增加模数V；另一方面，增加波长λ或者包层折射率（n2）可以减少模数。式（3.2.14）不包含包层直径，这说明它在各导模的传输中没有扮演重要的角色。在多模光纤中，光通过许多模传输，并且所有模主要局限在芯内传输。在阶跃折射率光纤中，一小部分基模场将进入包层传输。假如包层没有足够的厚度，这部分场将到达包层的最外边并泄漏出去，发生光能量的丢失。因此，通常阶跃单模光纤的包层直径至少是纤芯直径的10倍。
